COVID-19: A closer look
Hi there!
Curious about the math behind infection spread? I've posted a quick intro below.
COVID-19 vaccination efficacy in Ontario
The graph shows how much less likely vaccinated people are to become a positive COVID-19 case (case, green), be hospitalized whether in ICU or not (hospit, yellow), or to end up in ICU (icu, red), relative to people who are unvaccinated. Each point corresponds to the likelihood on that specific date. It fluctuates over time as, e.g., new strains like omicron come around or immunity wanes. The numbers in the legend on the right indicate the geometric mean likelihood over the last 20 days. Omicron began spreading widely in Ontario around December 10, 2021. As of March 10, 2022, Ontario reports cases in unvaccinated and those who have received 1-dose of a 2-dose vaccine as a single number which they describe as not fully vaccinated. Therefore, as of that date, it is not possible to compute the likelihood of becoming infected (green) for vaccinated relative to unvaccinated individuals.
Looking at the number of cases or hospitalization in vaccinated vs unvaccinated people alone, as reported, can be misleading. For example, if the vaccine is 90% effective and 70% of people are vaccinated, you expect 19% of cases to be in vaccinated people. To address this issue, the fraction of cases, hospitalizations and ICU admissions in (un)vaccinated people were rescaled based on the proportion of the population that was (un)vaccinated on the day the numbers were reported.
COVID-19 death per reported case in Ontario
(top left) number of COVID-19 deaths in one age group divided by all COVID-19 positive cases reported in that same age group. It is an estimate of the likelihood of dying of COVID-19 if you tested positive for COVID-19. You might think maybe other factors are important, like your health status, etc. While that might be true, it is also true that age is a good predictor of a mortal outcome (see bottom left).
(top right) the proportion of COVID-19 positive cases reported in one age group divided by the proportion of the Ontario population that is in that age group. The horizontal black line at 1/1 means the proportion of cases reported in that age group matches their proportion in the population. When an age group curve is above that black line, it means that age group is disproportionally over-represented in the number of positive cases reported. For example, when an age group curve reaches the first horizontal bar above the black line (2/1), it means that age group makes up a proportion of the reported positive cases that is 2 times higher than it should be. This would be the case, for example, if an age group that makes up 30% of the Ontario population represents 60% of positive cases reported. When a curve is below the black line, that age group is under-represented, they are reported as positive cases at a rate lower than we would expect, which is a good thing.
(bottom left) the orange dots are the actual % of reported COVID-19 positive cases that resulted in deaths (number of cases that were detected on that date that ultimately resulted in a death, divided by the total # of positive cases reported on that date with a known outcome [recovered or dead]). You can see that it was very high in our first wave (around 9.5%), then went down to about 1% over the summer, and is currently around 2%. The blue dots are the % of deaths predicted based only on the age of the # of positive cases reported that day (i.e. based on the odds of dying estimated in the top left graph). You can see that while age is not a perfect predictor (blue prediction points over/under estimate actual deaths in orange at times), it does account for most of the variation over time and for the shift from 9.5% to 1% to 2%. This means that other factors, such as health status, improvements in therapeutic interventions since 1st wave, etc., could play a role, in explaining the approx. 0.5%-1% variation in places where the prediction (blue) is not an excellent match for observations (orange). The 9.5% and 2% indicated on the graph corresponds to those used in the graphs below (Local scale) for Ontario.
The graphs were made from data for Ontario available publicly here.
Counts of new cases and deaths each day
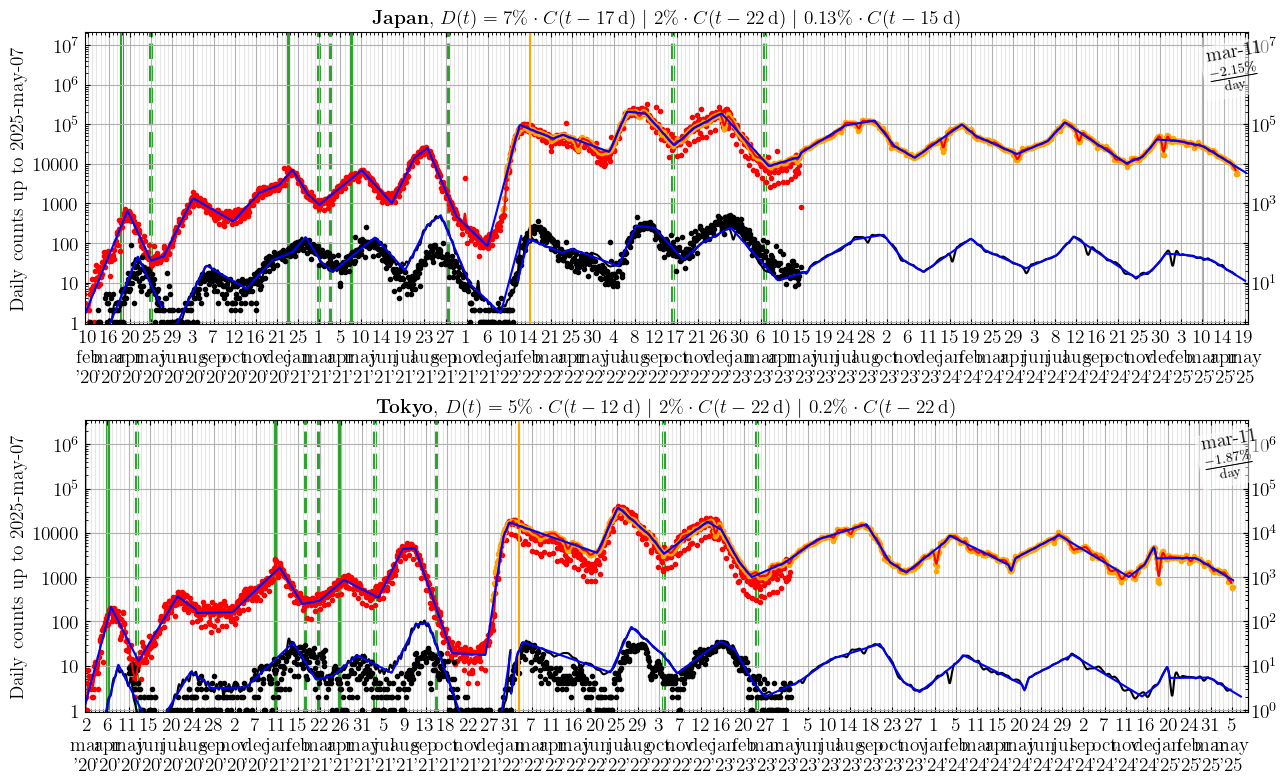
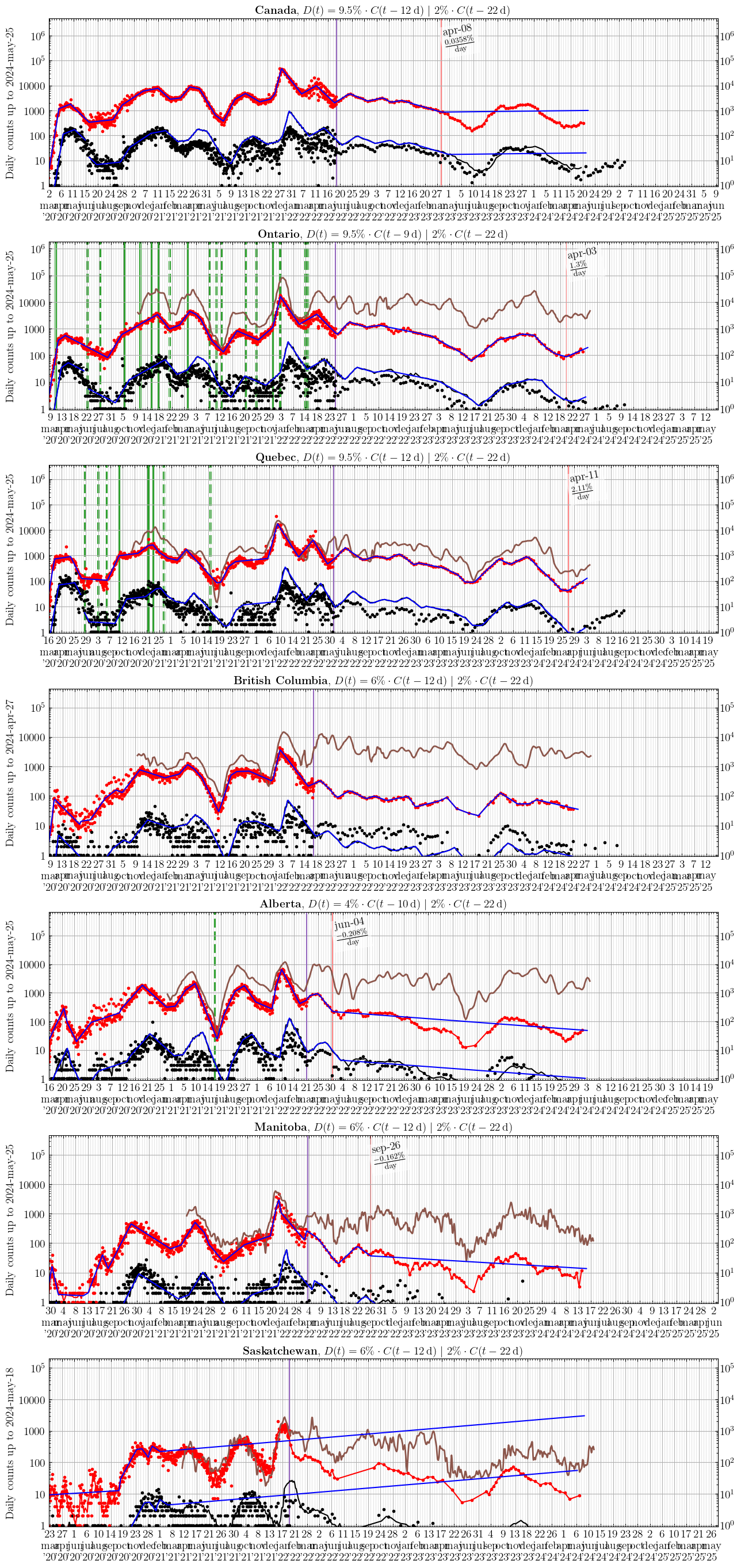
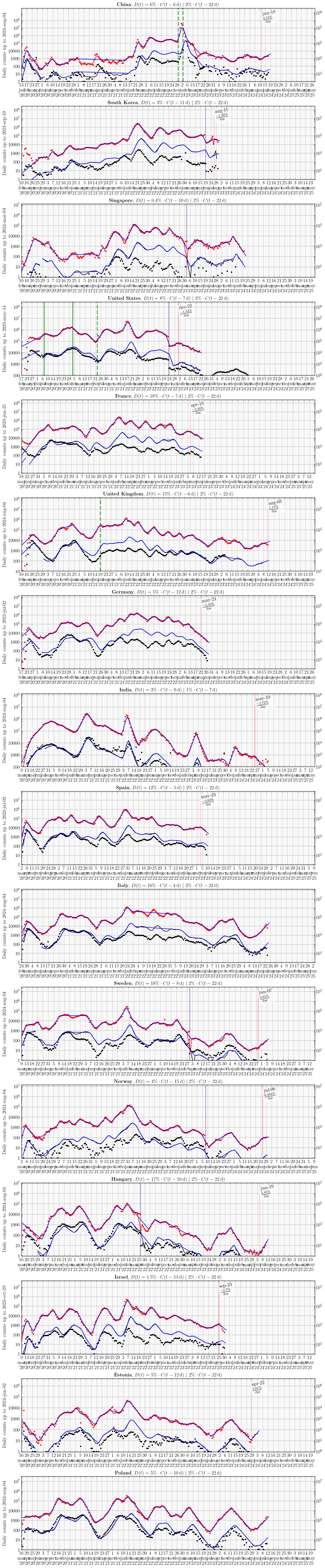
C stands for the daily new Cases (red), and D for the daily Deaths (black). The dots are the data, the (not always visible) red line is the smoothed data (Gaussian kernel, \(\sigma\)=2-4 days, applied to the log of the daily case count). The blue line is a set of linear segments identified via the method described by V. Muggeo, each corresponding to a period with a given rate of increase/decrease of daily counts, separated by vertical red dashed lines, likely corresponding to the start/end of certain public health measures. The black and blue lines for the daily death counts are the red and blue lines for the daily case counts shifted by eye by a # of days and multiplied by a percentage, indicated in the graph title. These #s suggest Japan (12 days between Case identified to Death, 5% of Cases result in Death) is possibly doing better than France (7 days Case to Death, 18% of Cases result in Death), because France seemingly takes 5 days more to report infected individuals as cases, and identifies 3-4 times fewer infected individuals as cases, assuming a similar likelihood of death from infection, which might not be correct.Japan and Tokyo
Canada and Provinces
Other countries
Data from:
World: https://covid.ourworldindata.org/data/owid-covid-data.csv
Canada: https://health-infobase.canada.ca/src/data/covidLive/covid19.csv
Japanese prefectures: https://github.com/reustle/covid19japan-data (up until 2022/sep/30) and then https://covid19.mhlw.go.jp/extensions/public/en
The math behind epidemiological infection spread
Simplistically, one can imagine the (unconstrained) growth rate early in the epidemic when everyone is susceptible is
\[ N(t) = N(0) \cdot R_0^{t/t_R} \]
where \( N(t) \) is the # of people infected at time \(t\), if there was \(N(0)\) people infected at time \(t=0\), and if each person infects \(R_0\) other people, and if the time between when you are infected and when you are no longer infectious (e.g. because you have died or recovered) is \(t_R\). Taking the \(\log_{10}\) on both sides you get:
\[ \begin{align*} \log_{10}[ N(t) ] &= \log_{10}[N(0)] + \frac{\log_{10}[R_0]}{t_R}\ t \\ y &= b + m x \end{align*} \]
You can perform a linear regression of \(y=\log_{10}[N(t)]\) versus \(x=t\), and you'll find that \(b=\log_{10}[N(0)]\) is your \(y\)-intercept, and \(m=\log_{10}[R_0]/t_R\) is your slope, as in \(y = b+mx\). This means that \(10^{m} = R_0^{(1\,\mathrm{day})/t_R}\) where \(t_R\) is in units of days, and then \(10^m\) is such that
\[ N(\mathrm{one\ day\ later}) = N(\mathrm{now}) \cdot 10^m \]So if \(10^m = 1.2\), it corresponds to a growth rate of 20%/day which is (\(10^m - 1)\cdot100\)%. You can use similar reasoning to compute the doubling time, the time \(t_\mathrm{doubling}\) (in days) such that \(R_0^{[t_\mathrm{doubling}/t_R]} = 2\). So \(t_\mathrm{doubling} = 2 t_R / \log_{10}(R_0)\).
Now what is this \(R_0\) all about? It is called the basic reproductive number (see the movie Contagion or Wikipedia). It is the number of people one infected person will infect over the period of time for which they were infectious, i.e. from the time they became infectious to the time they no longer are, if everyone they encounter is susceptible, assuming some average rate of encounter. But as we impose physical distancing measures, an infected person will encounter fewer people per day, and thus will not infect as many people during their infectious period. Say physical distancing measures mean you encounter half as many people as you used to, then you get something like:
\[ \begin{align*} N(t) &= N(0) \left(\frac{R_0}{2}\right)^{t/t_R} \\ m &= \frac{ \log_{10}\left[R_0/2 \right] }{t_R} \end{align*} \]so your slope suddenly changes when the effect of the physical distancing measures appears in the case counts, approximately a time \(t_R\) after it is introduced. So you can fit the data as a set of linear segments, with one linear regression for each segment corresponding to a new set of physical distancing measures. You can also estimate how effective the measure was by comparing the growth rate before and after the bend: that's what flattening the curve means.
Similarly, as the pandemic progresses, more and more of the people you encounter have already been infected, i.e. they have recovered, and they are presumably no longer susceptible because they have acquired (temporary?) immunity. This has an effect similar to physical distancing in that it reduces how many people you can infect over your infectious period, something like
\[ N(t) = N(0) \left[ R_0 \left(1 - \frac{C(t)}{\mathrm{Total}} \right) \right]^{t/t_R} \]where Total is the total population (e.g. of Ontario) so \([1 - C(t)/\mathrm{Total}]\) is the fraction of the population that is still susceptible (has not yet been infected), and \(C(t)\) is the cumulative number of all people infected thus far. So if \(2/3\) of the population has already been infected, you can only infect \(1/3\) as many people as you would have at the start of the pandemic when everyone was susceptible, \(R_0/3\).
Last modified: August 27, 2024, 22:45.
Webmaster:
